JUEGOS DE INGENIO DEL CLUB MENSA
SOLUCIONES 146 a 150
Solución 146: Breve encuentro.
Por: Josep María Albaigès.
Vamos a resolver este problema de forma gráfica. Para ello trazamos dos ejes de coordenadas, sobre uno de ellos marcamos el momento de llegada de Romeo y sobre el
otro el de Julieta, (véase la figura adjunta).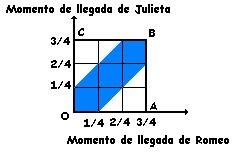



Las coordenadas de un punto cualquiera del interior del cuadrado OABC indicarán los momentos en que llegaron él y ella.

Es fácil ver que sólo se producen encuentros en los momentos que corresponden a cualquiera de los puntos que se hallan en el interior del hexágono sombreado.

La superficie total del cuadrado OABC, medida en cuadrados de lado 1/4, es de
3x3=9 unidades.

La superficie del hexágono sombreado vale 5 unidades.
Luego la probabilidad buscada es de 5/9 = 0,555 mayor que 1/2.
De una manera más general, si llamamos n al número de veces que el tiempo de
espera (en nuestro caso 1/4 de hora) está contenido en el tiempo de llegada (en nuestro
problema 3/4 de hora), la probabilidad de encuentro viene dada por la fórmula: (2n- 1)/n2
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 147: Gatos y ratones.
Por: Miquel Clusa
La velocidad comedora por gato es:


 

De donde resulta fácilmente:  gatos .
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 148: Cuadrado mágico de 5 y 7.
Por: Antonio Cebrián.

5555 7757 5775 7577
5777 7575 5557 7755
7557 5755 7777 5575
7775 5577 7555 5757

Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 149: Ecuación diofántica con soluciones palíndromas.
Por: Antonio Cebrián.


Resolviendo la ecuación en función de un parámetro "t" resulta:

x=3-57+7-57t x=171+399t
y=2-57+5-57t y=114+285t

Suponiendo que : x = abcba y = defed

171+399t = 10001a + 1010b + lOOc
114+285t = 10001d + 1010e - lOOf

    10001a +1010b +100c -171    10001d +1010e +100f -114
t= -------------------------- = -------------------------
          399                             285

50005a-70007d = 7070e - 5050b+ 700f- 500 c+ 57

5a - 7d -> tiene que terminar en 7

7 d + 7 termina en 5 ó 0 -> d=4 -> a=5

Por último por tanteo e=2, b=8 ,f=1 , c=9

x = 58985
y = 42124
Ver Enunciado de este problema
Este espacio ha sido dejado en blanco a propósito, para no descubrir accidentalmente la próxima solución. 
Solución 150: Cortando chapas
Por: Antonio Cebrián
Sea el triángulo equilátero ABC.



Trazando varias paralelas a la base ,BC , que cada una de ellas diste de la base 1,2,3,4 ... metros hasta llegar al vértice A.

El número de cuadrados será la suma de la parte entera de las medidas de las paralelas B1C1, B2C2, B3C3,....
hasta llegar a la última BnCn que sería = 1.

AH1=AH0-H1H0 = [(13 x 31/2)/2]  -  1

De la semejanza de triángulos:

B1C1   AHI
---- = ---
BOCO   AHO

B1C1= 13-2/31/2 -> Parte entera = 11
B2C2= 13-4/31/2 ->              = 10
B3C3= 13-6/31/2 ->              = 9

B7C7= 13-14/31/2->              = 4

BoCn= 13-20/31/2 -> ........... = 1

Suma de las partes enteras = 11+10+9+8+7+6+4+3+2+1 = 61

Ver Enunciado de este problema
(c) JGA, 1999 Los contenidos son de los autores, Mensa no sostiene ninguna idea Página principal